直角三角錐の4面の関係式 ー ピタゴラスの定理の拡張
【命題】
直角三角錐の頂点に接する側面の面積をA,B,Cとし、底面の面積をDとすると、
Aˆ(2)+Bˆ(2)+Cˆ(2)=Dˆ(2)
が成り立つ。
【メモ】
・ ˆは、べき乗(冪乗)記号とする。
・3次元直交座標の原点を頂点として、x,y,zの各座標軸上の3点を取れば直角三角錐となる。
【証明】
直角三角錐の頂点に接する各辺の長さをa,b,c、底面に接する各辺の長さをd,e,fとする。
d,eを長さとする二辺のなす角度をθとする。
辺と面の各名称の位置関係は下図の通りとする。
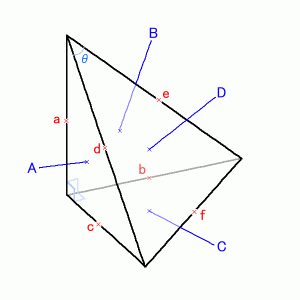
底面の面積の二乗
三角形の面積より、
D=1/2・deSinθ
Dˆ(2)=(dˆ(2)eˆ(2)Sinˆ(2)θ)/4
余弦定理より、
fˆ(2)=dˆ(2)+eˆ(2)−2deCosθ
Cosθ=(dˆ(2)+eˆ(2)−fˆ(2))/2de
二乗して、
Cosˆ(2)θ=(dˆ(2)+eˆ(2)−fˆ(2))/4dˆ(2)eˆ(2)=(2dˆ(2)eˆ(2)−2eˆ(2)fˆ(2)−2fˆ(2)dˆ(2)+dˆ(4)+eˆ(4)+fˆ(4))/4dˆ(2)eˆ(2)
Sinˆ(2)θ=1−Cosˆ(2)θ=(2dˆ(2)eˆ(2)+2eˆ(2)fˆ(2)+2fˆ(2)dˆ(2)−dˆ(4)−eˆ(4)−fˆ(4))/4dˆ(2)eˆ(2)
Sinˆ(2)θの式をDˆ(2)の式に代入して、
Dˆ(2)=(2dˆ(2)eˆ(2)+2eˆ(2)fˆ(2)+2fˆ(2)dˆ(2)−dˆ(4)−eˆ(4)−fˆ(4))/16 ・・・ 〔関係式1〕
頂点に接する面の面積の二乗の和
直角三角形の面積より、
A=(ca)/2, Aˆ(2)=(cˆ(2)aˆ(2))/4
B=(ab)/2, Bˆ(2)=(aˆ(2)bˆ(2))/4
C=(bc)/2, Cˆ(2)=(bˆ(2)cˆ(2))/4
ピタゴラスの定理より、
ア.dˆ(2)=cˆ(2)+aˆ(2)
イ.eˆ(2)=aˆ(2)+bˆ(2)
ウ.fˆ(2)=bˆ(2)+cˆ(2)
ア+イ−ウより、2aˆ(2)=dˆ(2)+eˆ(2)−fˆ(2)
イ+ウ−アより、2bˆ(2)=eˆ(2)+fˆ(2)−dˆ(2)
ウ+ア−イより、2cˆ(2)=fˆ(2)+dˆ(2)−eˆ(2)
面積の式にaˆ(2),bˆ(2),cˆ(2)を代入して、
Aˆ(2)=(fˆ(2)+dˆ(2)−eˆ(2))(dˆ(2)+eˆ(2)−fˆ(2))/16
=(2fˆ(2)eˆ(2)+dˆ(4)−eˆ(4)−fˆ(4))/16
Bˆ(2)=(dˆ(2)+eˆ(2)−fˆ(2))(eˆ(2)+fˆ(2)−dˆ(2))/16
=(2dˆ(2)fˆ(2)+eˆ(4)−dˆ(4)−fˆ(4))/16
Cˆ(2)=(eˆ(2)+fˆ(2)−dˆ(2))(fˆ(2)+dˆ(2)−eˆ(2))/16
=(2eˆ(2)dˆ(2)+fˆ(4)−dˆ(4)−eˆ(4))/16
したがって、
Aˆ(2)+Bˆ(2)+Cˆ(2)=(2dˆ(2)eˆ(2)+2eˆ(2)fˆ(2)+2fˆ(2)dˆ(2)−dˆ(4)−eˆ(4)−fˆ(4))/16 ・・・ 〔関係式2〕
結論
〔関係式1〕〔関係式2〕より、
Aˆ(2)+Bˆ(2)+Cˆ(2)=Dˆ(2) □
【問題】
1. ピタゴラスの定理は、2次元直交座標の原点を頂点として、x,yの各座標軸上の2点を取った直角三角形において成立し、上記関係式は、3次元直交座標の原点を頂点として、x,y,zの各座標軸上の3点を取った直角三角錐において成立する。
では、n次元直交座標の原点を頂点として、各座標軸上のn点を取ったn次元直角図形において、この関係式を拡張することができるか。
2. Aˆ(2)+Bˆ(2)=Cˆ(2)を満たす数の組について、そのような長さを三辺とする三角形は必ず存在するか。あればその三角形は直角三角形である。
同様に、Aˆ(2)+Bˆ(2)+Cˆ(2)=Dˆ(2)を満たす数の組について、そのような面積の三角錐は必ず存在するか。あればその三角錐は直角三角錐か。n次元においてはどうか。
【追記】
Aˆ(2)+Bˆ(2)=Cˆ(2), Aˆ(2)+Bˆ(2)+Cˆ(2)=Dˆ(2),・・・というピタゴラスの定理の拡張は、通常、n次元直交座標において原点を中心、式の左辺を成分、右辺を半径とする円,球・・・として捉える。ベクトルの成分と長さとしても捉えられるが、その幾何的根拠はともに、左辺を辺、右辺を対角線とする長方形,直方体,・・・である。この考え方では、任意のn次元で式と辺の長さが対応されているが、本ページの拡張では、2次元の場合には式と辺の長さが対応し、3次元の場合には式と側面の面積が対応している点が異なる。
参考:線形代数学、位相幾何学、単体
【問題2の前半解答】
問題2の前半「Aˆ(2)+Bˆ(2)=Cˆ(2)を満たす数の組について、そのような長さを三辺とする三角形は必ず存在するか。あればその三角形は直角三角形である。」
Aˆ(2)+Bˆ(2)=Cˆ(2)を満たす数の組があるとき、2次元直交座標に原点を中心として半径Cの円を取れば、(A,B)の点は半径Cの円上にある。(A,B)と原点を結ぶ直線、(A,B)から各座標軸への垂線(と平行線)、これら三直線を3辺とする三角形を取れば、3辺の長さはA,B,Cである。
さらに、A,B,Cを三辺の長さとする三角形が他にあるとすると、
長さCの辺の対角の角度をθとすると、余弦定理より、
Cˆ(2)=Aˆ(2)+Bˆ(2)−2ABCosθ
である。
三角形なので0°<θ<180°において、Cosθ=0となるのは、θ=90°のみであり、
Cˆ(2)=Aˆ(2)+Bˆ(2)が成立すれば、その三角形もやはり直角三角形である。 □
【追記2】
Wikipediaによると、本定理はDe Gua’s theoremと呼ばれ古くはルネ・デカルトの時代には知られていたらしい。未だ様々な論点が残されていると思われ、興味深い。
参考ページ(英語):De Gua’s theorem、Trirectangular tetrahedron
公開日:2017/5/7
修正日:2017/5/13 最後尾に参考を追加。
修正日:2017/5/15 【追記】を追加。
修正日:2017/5/16 【追記】「本ページでは、」⇒「本ページの拡張では、」
修正日:2017/5/16 最後尾に【問題2の前半解答】を追加。
修正日:2023/6/16 【追記2】を追加。
最終修正日:2023/6/16



